Définition de la fonction exponentielle

La fonction exponentielle modélise divers phénomènes naturels et situations sociales et économiques, c'est pourquoi il est important d'identifier des fonctions exponentielles dans divers contextes.

Rappelons que pour un nombre \({a^1} = a,{a^2} = aa,\;{a^3} = aaa\) est défini, en général on a que pour tout \(n\ ) nombre naturel :

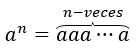
Dans le cas \(a \ne 0\), on a que: \({a^0} = 1,\;\) en fait, quand \(a \ne 0,\) il est logique de faire l'opération \ (\frac{a}{a} = 1;\) en appliquant la loi des exposants, on a :

\(\frac{a}{a} = 1\)

\({a^{1 – 1}} = 1\)

\({a^0} = 1.\)

Lorsque \(a = 0\), le raisonnement précédent n'a pas de sens, par conséquent, l'expression \({0^0},\) n'a pas d'interprétation mathématique.

Dans le cas où \(b > 0\) et s'il est vrai que \({b^n} = a,\) on dit que \(b\) est la nième racine de \(a\) et est généralement noté \ (b = {a^{\frac{1}{n}}},\;\) ou \(b = \sqrt[n]{a}\).

Lorsque \(a < 0\), il n'y a pas de nombre réel \(b\) tel que \({b^2} = a;\) car \({b^2} \ge 0;\;\ ) donc expressions de la forme \({a^{\frac{m}{n}}}\), ne sera pas considéré pour \(a < 0.\) Dans l'expression algébrique suivante: \({a^n}\) \(a \ ) est appelé base, et \(n\) est appelé exposant, \({a^n}\)est appelé la puissance\(\;n\) de \(a\) ou est aussi appelé \(a\) à la puissance \(n,\;\)se respecter les lois suivantes des exposants:

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\gauche({ab} \droite)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) pour chaque \(a \ne 0\)

La fonction exponentielle est de la forme :

\(f\gauche( x \droite) = {a^x}\)

où \(a > 0\) est une constante et la variable indépendante est l'exposant \(x\).

Pour faire une analyse de la fonction exponentielle, nous allons considérer trois cas

Cas 1 Lorsque la base \(a = 1.\)

Dans ce cas, \(a = 1,\) la fonction \(f\left( x \right) = {a^x}\) est une fonction constante.

Cas 2 Lorsque la base \(a > 1\)

Dans ce cas, nous avons ce qui suit :

Valeur de \(x\)
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(une < {a^x}\)

La fonction \(f\left( x \right) = {a^x}\) est une fonction strictement croissante, c'est-à-dire si \({x_2} > {x_1}\), alors :

\({a^{{x_2}}} > a_{}^{{x_2}}\)

\(f\gauche( {{x_2}} \droite) > f\gauche( {{x_1}} \droite)\)

Lorsqu'un phénomène est modélisé par une fonction exponentielle, avec \(a > 1\), on dit qu'il présente une croissance exponentielle.

Cas 2 Lorsque la base \(a < 1\).

Valeur de \(x\)
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < une < 1\)

Cuando \(a < 1\), la función \(f\left( x \right) = {a^x}\) es una función estrictamente de decreciente, es decir, si \({x_2} > {x_1}\ ), ensuite:

\({a^{{x_2}}} < a_{}^{{x_1}}\) \(f\left( {{x_2}} \right) < f\left( {{x_1}} \right) \) Lorsqu'un phénomène est modèles avec une fonction exponentielle, avec \(a < 1\), on dit qu'il présente une décroissance ou décroissance exponentiel. Le graphique suivant illustre le comportement de \({a^x}\), dans ses trois cas différents.

Applications de la fonction exponentielle

Exemple 1 Croissance démographique

On notera \({P_0}\) la population initiale et \(r \ge 0\) le taux de croissance de la population, si le taux de population reste constant dans le temps; la fonction

\(P\left( t \right) = {P_0}{\left( {1 + r} \right)^t};\)

Trouver la population au temps t.

Exemple pratique 1

La population du Mexique, en l'an 2021 est de 126 millions et a présenté une croissance annuelle de 1,1%, Si cette croissance se maintient, quelle sera la population du Mexique en l'an 2031, en l'an 2021?

Solution

Dans ce cas \({P_o} = 126\) et \(r = \frac{{1.1}}{{100}} = 0.011\), vous devez donc utiliser :

\(P\left( t \right) = {P_0}{\left( {1 + .0011} \right)^t}\)

Le tableau suivant montre les résultats

Année	temps écoulé (\(t\))	Calcul	Population (millions)
2021	0	\(P\left( t \right) = 126{\left( {1.0011} \right)^0}\)	126
2031	10	\(P\left( t \right) = 126{\left( {1.0011} \right)^{10}}\)	140.57
2051	30	\(P\left( t \right) = 126{\left( {1.0011} \right)^{30}}\)	174.95

Exemple 2 Calcul des intérêts composés

Les banques proposent un taux d'intérêt annuel, mais le taux réel dépend du nombre de mois pendant lesquels vous l'investissez; Par exemple, si on vous propose un taux d'intérêt annuel de r %, le taux mensuel réel est de \(\frac{r}{{12}}\) %, le taux bimestriel est \(\frac{r}{6}\) %, trimestriel est \(\frac{r}{4}\) %, trimestriel est \(\frac{r}{3}\) % et le semestre est \(\frac{r}{2}\) %.

Exemple pratique 2

Supposons que vous investissiez 10 000 dans une banque et qu'elle vous offre les taux d'intérêt annuels suivants :

Dépôts à terme	Taux annuel	périodes dans une année	taux réel	Argent accumulé en \(k\) mois
deux mois	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0.00091667} \right)^{\frac{k}{2}}}\)
trois mois	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0.00461667} \right)^{\frac{k}{3}}}\)
six mois	1.56%	2	\(\frac{{1.56\% }}{4} = 0.78{\rm{\% }}\)	\(10000{\left( {1 + 0.0078} \right)^{\frac{k}{6}}}\)

Le nombre \(e\), l'intérêt constant et continu d'Euler.

Supposons maintenant que nous ayons un capital initial \(C\) et que nous l'investissions à taux fixe \(r > 0\), et que nous divisons l'année en \(n\) périodes; le capital accumulé en une année est égal à :

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)

Pour analyser comment le capital accumulé se comporte lorsque \(n\), croît, nous allons réécrire le capital accumulé, en un an :

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)\(A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},\)

en faisant \(m = \frac{n}{r}\), on obtient :

\(A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}\)\(A = C{\left( {{{\left( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.\)

À mesure que \(n\) grandit, il en va de même pour \(m = \frac{n}{r}.\)

Au fur et à mesure que \(m = \frac{n}{r},\) grandit, l'expression \({\left( {1 + \frac{1}{m}} \right)^m}\) se rapproche de ce qu'on appelle le Constante d'Euler ou nombre :

\(e \environ 2,718281828 \ldots .\)

La constante d'Euler n'a pas d'expression décimale finie ou périodique.

On a les approximations suivantes

\(C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \approx C{e^r},\) \(C{\left( {1 + \frac{r}{n}} \right)^{ns}} \approx C{e^{rs}}.\)

A l'expression :

\(A = \;C{e^r},\)

Nous pouvons l'interpréter de deux manières :

1.- Comme le montant maximum que nous pouvons accumuler en un an lorsque nous investissons du capital \(C,\;\) à un taux annuel \(r.\)

2.- Comme le montant que nous accumulerions, en un an, si notre capital était continuellement réinvesti à un rythme annuel \(r.\)

\(T\left( s \right) = \;C{e^{rs}},\)

est le montant accumulé si \(s\) années sont investies avec un intérêt continu.

Exemple concret 3

Nous allons maintenant revenir à une partie de l'exemple concret 2, où le taux annuel est de 0,55 % en versements bimestriels. Calculez le capital qui s'accumule si le capital initial est de 10 000 et réinvestit six mois, deux ans, 28 mois.

\(10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525\)

comme le montre le tableau ci-dessous, la valeur de \(m = \frac{n}{r},\) n'est pas "petite" et le tableau ci-dessus indique que \({\left( {1 + \frac{1}{ m}} \right)^m}\) est proche de la constante d'Euler.

Temps	Nombre de périodes (\(k\))	Capital accumulé, en milliers, réinvesti tous les deux mois
Demi-année	3	\(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\)
Deux ans	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 mois	19	\(10{\left( {1.00091667} \right)^{19}} = 10.\;175612\)

Temps	Période des années (\(s\))	Capital accumulé, en milliers, investir avec intérêt continu
Demi-année	\(s = \frac{1}{2}\)	\(10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
Deux ans	\(s = 2\)	\(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 mois	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

Exemple 2 Amortissement

Exemple pratique 1

Un ordinateur se déprécie de 30 % chaque année. Si un ordinateur coûte 20 000 pesos, déterminez le prix de l'ordinateur pendant \(t = 1,12,\;14,\;38\) mois.

Dans ce cas, on a :

\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0.30} \right)^t}\)

Avec \(t\) en années, remplacer \(t\) dans le tableau suivant donne

temps en mois	temps en années	calculs	Valeur numérique
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859