Definizione di funzione esponenziale

Inibizione Teoria Delle Stringhe / by admin / April 02, 2023

Marco Antonio Rodríguez Andrade
Maestro di Matematica, Dottore in Scienze

La funzione esponenziale modella vari fenomeni naturali e situazioni sociali ed economiche, motivo per cui è importante identificare le funzioni esponenziali in vari contesti.

Ricordiamo che per un numero definito ${a^1} = a,{a^2} = aa,\;{a^3} = aaa$, in generale si ha che per ogni \(n\ ) numero naturale:

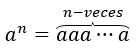
Nel caso $a \ne 0$, abbiamo che: ${a^0} = 1,\;$ infatti, quando $a \ne 0,$ ha senso eseguire l'operazione \ (\frac{a}{a} = 1;\) applicando la legge degli esponenti si ha:

$\frac{a}{a} = 1$

${a^{1 – 1}} = 1$

${a^0} = 1.$

Quando $a = 0$, il ragionamento precedente non ha senso, quindi, l'espressione ${0^0},$ manca di interpretazione matematica.

Nel caso in cui $b > 0$ ed è vero che ${b^n} = a,$ si dice che $b$ è l'ennesima radice di $a$ e di solito è indicato come \ (b = {a^{\frac{1}{n}}},\;\) o $b = \sqrt[n]{a}$.

Quando $a < 0$, non esiste un numero reale $b$ tale che ${b^2} = a;$ perché ${b^2} \ge 0;\;\ ) quindi espressioni della forma \({a^{\frac{m}{n}}}$, non sarà considerato per $a < 0.$ Nella seguente espressione algebrica: ${a^n}$ $a \ ) si chiama base, e \(n$ lo è chiamato esponente, ${a^n}$è chiamato la potenza$\;n$ di $a$ o è anche chiamato $a$ alla potenza $n,\;$se rispettare le seguenti leggi degli esponenti:

instagram story viewer

${a^n}{a^m} = {a^{n + m}}$	$\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}$	${\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}$
$\frac{1}{{{a^n}}} = {a^{ – n}}$	${a^n} = \frac{1}{{{a^{ – n}}}}$	${\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}$
${\sinistra( {ab} \destra)^n} = {a^n}{b^n}$	${\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}$	${a^0} = 1$ per ogni $a \ne 0$

La funzione esponenziale è della forma:

$f\sinistra( x \destra) = {a^x}$

dove $a > 0$ è una costante e la variabile indipendente è l'esponente $x$.

Per fare un'analisi della funzione esponenziale, prenderemo in considerazione tre casi

Caso 1 Quando la base $a = 1.$

In questo caso, $a = 1,$ la funzione $f\left( x \right) = {a^x}$ è una funzione costante.

Caso 2 Quando la base $a > 1$

In questo caso, abbiamo quanto segue:

Valore di $x$
$x<0$	$0 < {a^x} < 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	\(1 < {a^x}
$x = 1$	${a^x} = 1$
$x > 1$	$a < {a^x}$

La funzione $f\left( x \right) = {a^x}$ è una funzione strettamente crescente, cioè, se ${x_2} > {x_1}$, allora:

${a^{{x_2}}} > a_{}^{{x_2}}$

$f\sinistra( {{x_2}} \destra) > f\sinistra( {{x_1}} \destra)$

Quando un fenomeno è modellato con una funzione esponenziale, con $a > 1$, diciamo che presenta una crescita esponenziale.

Caso 2 Quando la base $a < 1$.

Valore di $x$
$x<0$	${a^x} > 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$0 < {a^x} < 1$
$x = 0$	${a^x} = 1$
$x > 1$	\(0 < {a^x}

Quando $a < 1$, la funzione $f\left( x \right) = {a^x}$ è una funzione strettamente decrescente, cioè se \({x_2} > {x_1}\ ), COSÌ:

${a^{{x_2}}} < a_{}^{{x_1}}$ $f\sinistra( {{x_2}} \right) < f\sinistra( {{x_1}} \right) $ Quando un fenomeno è modelli con una funzione esponenziale, con $a < 1$, diciamo che presenta un decadimento o decremento esponenziale. Il grafico seguente illustra il comportamento di ${a^x}$, nei suoi tre diversi casi.

Applicazioni della funzione esponenziale

Esempio 1 Crescita della popolazione

Indicheremo con ${P_0}$ la popolazione iniziale e con $r \ge 0$ il tasso di crescita della popolazione, se il tasso di popolazione rimane costante nel tempo; la funzione

$P\sinistra( t \destra) = {P_0}{\sinistra( {1 + r} \destra)^t};$

Trova la popolazione al tempo t.

Esempio pratico 1

La popolazione del Messico, nell'anno 2021 è di 126 milioni e ha presentato una crescita annua dell'1,1%, Se questa crescita viene mantenuta, quale popolazione ci sarà in Messico nell'anno 2031, nell'anno 2021?

Soluzione

In questo caso ${P_o} = 126$ e $r = \frac{{1.1}}{{100}} = 0.011$, quindi dovresti usare:

$P\sinistra( t \destra) = {P_0}{\sinistra( {1 + .0011} \destra)^t}$

La tabella seguente mostra i risultati

Anno	tempo trascorso ($T$)	Calcolo	Popolazione (milioni)
2021	0	$P\sinistra( t \destra) = 126{\sinistra( {1.0011} \destra)^0}$	126
2031	10	$P\sinistra( t \destra) = 126{\sinistra( {1.0011} \destra)^{10}}$	140.57
2051	30	$P\sinistra( t \destra) = 126{\sinistra( {1.0011} \destra)^{30}}$	174.95

Esempio 2 Calcolo dell'interesse composto

Le banche offrono un tasso di interesse annuale, ma il tasso reale dipende da quanti mesi lo investi; Ad esempio, se ti viene offerto un tasso di interesse annuo di r%, il tasso mensile reale è $\frac{r}{{12}}$%, il tasso bimestrale è $\frac{r}{6}$%, trimestrale è $\frac{r}{4}$%, trimestrale è $\frac{r}{3}$%, e il semestre è $\frac{r}{2}$%.

Esempio pratico 2

Supponi di investire 10.000 in una banca e ti offrono i seguenti tassi di interesse annuali:

Depositi a tempo determinato	Rata annuale	periodi in un anno	tasso effettivo	Denaro accumulato in $k$ mesi
due mesi	0.55%	6	$\frac{{0.55\% }}{6} = 0.091667{\rm{\% }}$	$10000{\left( {1 + 0.00091667} \right)^{\frac{k}{2}}}$
tre mesi	1.87%	4	$\frac{{1.87\% }}{4} = 0.4675{\rm{\% }}$	$10000{\left( {1 + 0.00461667} \right)^{\frac{k}{3}}}$
sei mesi	1.56%	2	$\frac{{1.56\% }}{4} = 0.78{\rm{\% }}$	$10000{\left( {1 + 0.0078} \right)^{\frac{k}{6}}}$

Il numero $e$, l'interesse costante e continuo di Eulero.

Supponiamo ora di avere un capitale iniziale $C$ e lo investiamo a tasso fisso $r > 0$, e dividiamo l'anno in $n$ periodi; il capitale accumulato in un anno è pari a:

$A = \;C{\left( {1 + \frac{r}{n}} \right)^n}$

Per analizzare come si comporta il capitale accumulato quando $n$, cresce, riscriveremo il capitale accumulato, in un anno:

$A = \;C{\left( {1 + \frac{r}{n}} \right)^n}$$A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},$

facendo $m = \frac{n}{r}$, otteniamo:

$A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}$$A = C{\left( {{{\left( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.$

Al crescere di $n$, cresce anche $m = \frac{n}{r}.$

Al crescere di $m = \frac{n}{r},$ l'espressione ${\left( {1 + \frac{1}{m}} \right)^m}$ si avvicina a quella che viene chiamata Costante o numero di Eulero:

$e \circa 2.718281828 \ldots .$

La costante di Eulero non ha un'espressione decimale finita o periodica.

Abbiamo le seguenti approssimazioni

$C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \circa C{e^r},$ $C{\left( {1 + \frac{r}{n}} \right)^{ns}} \circa C{e^{rs}}.$

All'espressione:

$A = \;C{e^r},$

Possiamo interpretarlo in due modi:

1.- Come importo massimo che possiamo accumulare in un anno quando investiamo capitale $C,\;$ a un tasso annuo $r.$

2.- Come l'importo che accumuleremmo, in un anno, se il nostro capitale fosse continuamente reinvestito ad un tasso annuo $r.$

$T\sinistra( s \destra) = \;C{e^{rs}},$

è l'importo accumulato se $s$ anni sono investiti con interessi continui.

Esempio concreto 3

Torniamo ora a una parte dell'esempio concreto 2, dove il tasso annuo è dello 0,55% in rate bimestrali. Calcola il capitale che si accumula se il capitale iniziale è di 10.000 e si reinvestisce mezzo anno, due anni, 28 mesi.

$10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525$

come mostra la tabella sottostante, il valore di $m = \frac{n}{r},$ non è “piccolo” e la tabella sopra indica che ${\left( {1 + \frac{1}{ m}} \right)^m}$ è vicino alla costante di Eulero.

Tempo	Numero di periodi ($k$)	Capitale accumulato, in migliaia, reinvestito ogni due mesi
Metà anno	3	$10{\sinistra( {1.00091667} \destra)^3} = 10.{\rm{\;}}027525$
Due anni	12	$10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557$
38 mesi	19	$10{\sinistra( {1.00091667} \destra)^{19}} = 10.\;175612$

Tempo	Tempo di anni ($s$)	Capitale accumulato, in migliaia, investito con interesse continuo
Metà anno	$s = \frac{1}{2}$	$10{e^{0.0055\sinistra( {\frac{1}{2}} \destra)}} = 10.{\rm{\;}}027538$
Due anni	$s = 2$	$10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607$
38 mesi	$s = \frac{{19}}{6}$	$10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692$

Esempio 2 Ammortamento

Esempio pratico 1

Un computer si deprezza del 30% ogni anno, se un computer costa $ 20.000 pesos, determinare il prezzo del computer per $t = 1,12,\;14,\;38$ mesi.

In questo caso si ha:

$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0.30} \right)^t}$

Con $t$ in anni, sostituendo $t$ nella tabella seguente si ottiene

tempo in mesi	tempo in anni	calcoli	Valore numerico
1	$\frac{1}{{12}}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}$	19414.289
12	1	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}$	14000
14	$\frac{7}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	13192.012
38	$\frac{{19}}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	6464.0859

Tag nuvola

Valutazione

Visualizzazioni

Commenti

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\sinistra( {ab} \destra)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) per ogni \(a \ne 0\)

Valore di \(x\)
\(x<0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x}
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Valore di \(x\)
\(x<0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x}

Tempo	Tempo di anni (\(s\))	Capitale accumulato, in migliaia, investito con interesse continuo
Metà anno	\(s = \frac{1}{2}\)	\(10{e^{0.0055\sinistra( {\frac{1}{2}} \destra)}} = 10.{\rm{\;}}027538\)
Due anni	\(s = 2\)	\(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 mesi	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

Anno	tempo trascorso (\(T\))	Calcolo	Popolazione (milioni)
2021	0	\(P\sinistra( t \destra) = 126{\sinistra( {1.0011} \destra)^0}\)	126
2031	10	\(P\sinistra( t \destra) = 126{\sinistra( {1.0011} \destra)^{10}}\)	140.57
2051	30	\(P\sinistra( t \destra) = 126{\sinistra( {1.0011} \destra)^{30}}\)	174.95

Depositi a tempo determinato	Rata annuale	periodi in un anno	tasso effettivo	Denaro accumulato in \(k\) mesi
due mesi	0.55%	6	\(\frac{{0.55\% }}{6} = 0.091667{\rm{\% }}\)	\(10000{\left( {1 + 0.00091667} \right)^{\frac{k}{2}}}\)
tre mesi	1.87%	4	\(\frac{{1.87\% }}{4} = 0.4675{\rm{\% }}\)	\(10000{\left( {1 + 0.00461667} \right)^{\frac{k}{3}}}\)
sei mesi	1.56%	2	\(\frac{{1.56\% }}{4} = 0.78{\rm{\% }}\)	\(10000{\left( {1 + 0.0078} \right)^{\frac{k}{6}}}\)

Tempo	Numero di periodi (\(k\))	Capitale accumulato, in migliaia, reinvestito ogni due mesi
Metà anno	3	\(10{\sinistra( {1.00091667} \destra)^3} = 10.{\rm{\;}}027525\)
Due anni	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 mesi	19	\(10{\sinistra( {1.00091667} \destra)^{19}} = 10.\;175612\)

tempo in mesi	tempo in anni	calcoli	Valore numerico
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859