Definição de Função Exponencial

Inibição Teoria Das Cordas / by admin / April 02, 2023

protection click fraud

Marco Antonio Rodrigues Andrade
Mestre em Matemática, Doutor em Ciências

A função exponencial modela vários fenômenos naturais e situações sociais e econômicas, por isso é importante identificar funções exponenciais em vários contextos.

Lembremos que para um número ${a^1} = a,{a^2} = aa,\;{a^3} = aaa$ está definido, em geral temos que para qualquer \(n\ ) número natural:

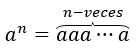
No caso $a \ne 0$, temos que: ${a^0} = 1,\;$ de fato, quando $a \ne 0,$ faz sentido fazer a operação \ (\frac{a}{a} = 1;\) aplicando a lei dos expoentes, temos:

$\frac{a}{a} = 1$

${a^{1 – 1}} = 1$

${a^0} = 1.$

Quando $a = 0$, o raciocínio anterior não faz sentido, portanto, a expressão ${0^0},$ carece de interpretação matemática.

No caso de $b > 0$ e é verdade que ${b^n} = a,$ diz-se que $b$ é a enésima raiz de $a$ e geralmente é denotado como \ (b = {a^{\frac{1}{n}}},\;\) ou $b = \sqrt[n]{a}$.

Quando $a < 0$, não existe nenhum número real $b$ tal que ${b^2} = a;$ porque ${b^2} \ge 0;\;\ ) então expressões da forma \({a^{\frac{m}{n}}}$, não será considerado para $a < 0.$ Na seguinte expressão algébrica: ${a^n}$ $a \ ) é chamado de base e \(n$ é chamado de expoente, ${a^n}$é chamado de potência$\;n$ de $a$ ou também é chamado de $a$ elevado a $n,\;$se cumprir as seguintes leis dos expoentes:

instagram story viewer

${a^n}{a^m} = {a^{n + m}}$	$\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}$	${\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}$
$\frac{1}{{{a^n}}} = {a^{ – n}}$	${a^n} = \frac{1}{{{a^{ – n}}}}$	${\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}$
${\left( {ab} \right)^n} = {a^n}{b^n}$	${\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}$	${a^0} = 1$ para cada $a \ne 0$

A função exponencial é da forma:

$f\esquerda( x \direita) = {a^x}$

onde $a > 0$ é uma constante e a variável independente é o expoente $x$.

Para fazer uma análise da função exponencial, vamos considerar três casos

Caso 1 Quando a base $a = 1.$

Neste caso, $a = 1,$ a função $f\left( x \right) = {a^x}$ é uma função constante.

Caso 2 Quando a base $a > 1$

Neste caso, temos o seguinte:

Valor de $x$
$x < 0$	$0 < {a^x} < 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$1 < {a^x} < a$
$x = 1$	${a^x} = 1$
$x > 1$	$a < {a^x}$

A função $f\left( x \right) = {a^x}$ é uma função estritamente crescente, ou seja, se ${x_2} > {x_1}$, então:

${a^{{x_2}}} > a_{}^{{x_2}}$

$f\left( {{x_2}} \right) > f\left( {{x_1}} \right)$

Quando um fenômeno é modelado com uma função exponencial, com $a > 1$, dizemos que ele apresenta crescimento exponencial.

Caso 2 Quando a base $a < 1$.

Valor de $x$
$x < 0$	${a^x} > 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$0 < {a^x} < 1$
$x = 0$	${a^x} = 1$
$x > 1$	$0 < {a^x} < a < 1$

Quando $a < 1$, a função $f\left( x \right) = {a^x}$ é uma função estritamente decrescente, ou seja, se \({x_2} > {x_1}\ ), então:

${a^{{x_2}}} < a_{}^{{x_1}}$ $f\left( {{x_2}} \right) < f\left( {{x_1}} \right) $ Quando um fenômeno é modelos com função exponencial, com $a < 1$, dizemos que apresenta decaimento ou decréscimo exponencial. O gráfico a seguir ilustra o comportamento de ${a^x}$, em seus três casos diferentes.

Aplicações da função exponencial

Exemplo 1 Crescimento populacional

Denotaremos com ${P_0}$ a população inicial e com $r \ge 0$ a taxa de crescimento populacional, se a taxa populacional permanecer constante ao longo do tempo; a função

$P\esquerda( t \direita) = {P_0}{\esquerda( {1 + r} \direita)^t};$

Encontre a população no tempo t.

Exemplo prático 1

A população do México, no ano de 2021 é de 126 milhões e apresentou um crescimento anual de 1,1%, Se esse crescimento for mantido, que população haverá no México no ano de 2031, no ano 2021?

Solução

Neste caso ${P_o} = 126$ e $r = \frac{{1.1}}{{100}} = 0.011$, então você deve usar:

$P\esquerda( t \direita) = {P_0}{\esquerda( {1 + .0011} \direita)^t}$

A tabela a seguir mostra os resultados

Ano	Tempo decorrido ($t$)	Cálculo	População (milhões)
2021	0	$P\left( t \right) = 126{\left( {1.0011} \right)^0}$	126
2031	10	$P\left( t \right) = 126{\left( {1.0011} \right)^{10}}$	140.57
2051	30	$P\left( t \right) = 126{\left( {1.0011} \right)^{30}}$	174.95

Exemplo 2 Cálculo de juros compostos

Os bancos oferecem uma taxa de juros anual, mas a taxa real depende de quantos meses você investe; Por exemplo, se lhe for oferecida uma taxa de juros anual de r%, a taxa mensal real é $\frac{r}{{12}}$%, a taxa bimestral é $\frac{r}{6}$%, trimestral é $\frac{r}{4}$%, trimestral é $\frac{r}{3}$% e semestral é $\frac{r}{2}$%.

Exemplo prático 2

Suponha que você invista 10.000 em um banco e eles lhe ofereçam as seguintes taxas de juros anuais:

Depósitos a prazo fixo	Taxa anual	períodos em um ano	taxa real	Dinheiro acumulado em $k$ meses
dois meses	0.55%	6	$\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}$	$10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}$
três meses	1.87%	4	$\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}$	$10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}$
seis meses	1.56%	2	$\frac{{1,56\% }}{4} = 0,78{\rm{\% }}$	$10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}$

O número $e$, constante e contínua de Euler.

Agora suponha que temos um capital inicial $C$ e o investimos a uma taxa fixa $r > 0$, e dividimos o ano em $n$ períodos; o capital acumulado em um ano é igual a:

$A = \;C{\esquerda( {1 + \frac{r}{n}} \direita)^n}$

Para analisar como se comporta o capital acumulado quando $n$, cresce, vamos reescrever o capital acumulado, em um ano:

$A = \;C{\esquerda( {1 + \frac{r}{n}} \direita)^n}$$A = \;C{\esquerda( {1 + \frac{1} {{\frac{n}{r}}}} \direita)^{\esquerda( {\frac{n}{r}} \direita) r}},$

fazendo $m = \frac{n}{r}$, obtemos:

$A = C{\esquerda( {1 + \frac{1}{m}} \direita)^{mr}}$$A = C{\esquerda( {{{\esquerda( {1 + \ frac{1}{m}} \direita)}^m}} \direita)^r}.$

Conforme $n$ cresce, $m = \frac{n}{r} também cresce.$

À medida que $m = \frac{n}{r},$ cresce a expressão ${\left( {1 + \frac{1}{m}} \right)^m}$ se aproxima do que é chamado de Constante ou número de Euler:

$e \approx 2.718281828 \ldots .$

A constante de Euler não possui uma expressão decimal finita ou periódica.

Temos as seguintes aproximações

$C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \approx C{e^r},$ $C{\esquerda( {1 + \frac{r}{n}} \direita)^{ns}} \approx C{e^{rs}}.$

Para a expressão:

$A = \;C{e^r},$

Podemos interpretá-lo de duas maneiras:

1.- Como o valor máximo que podemos acumular em um ano quando investimos capital $C,\;$ a uma taxa anual $r.$

2.- Como o valor que acumularíamos, em um ano, se nosso capital fosse continuamente reinvestido a uma taxa anual $r.$

$T\left( s \right) = \;C{e^{rs}},$

é o valor acumulado se $s$ anos forem investidos com juros contínuos.

Exemplo concreto 3

Agora voltaremos a uma parte do exemplo concreto 2, onde a taxa anual é de 0,55% em parcelas bimestrais. Calcule o capital que acumula se o capital inicial for 10.000 e reinvestir meio ano, dois anos, 28 meses.

$10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525$

como mostra a tabela abaixo, o valor de $m = \frac{n}{r},$ não é “pequeno” e a tabela acima indica que ${\left( {1 + \frac{1}{ m}} \right)^m}$ está próximo da constante de Euler.

Tempo	Número de períodos ($k$)	Capital acumulado, em milhares, reinvestido a cada dois meses
Meio ano	3	$10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525$
Dois anos	12	$10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557$
38 meses	19	$10{\left( {1.00091667} \right)^{19}} = 10.\;175612$

Tempo	Tempo dos anos ($s$)	Capital acumulado, em milhares, invista com juros contínuos
Meio ano	$s = \frac{1}{2}$	$10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538$
Dois anos	$s = 2$	$10{\left( {1,00091667} \right)^{0,0055\left( 2 \right)}} = 10110.{\rm{\;}}607$
38 meses	$s = \frac{{19}}{6}$	$10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692$

Exemplo 2 Depreciação

Exemplo prático 1

Um computador desvaloriza 30% a cada ano, se um computador custa $ 20.000 pesos, determine o preço do computador para $t = 1,12,\;14,\;38$ meses.

Neste caso, tem-se:

$P\esquerda( t \direita) = 20000{\rm{\;}}{\esquerda( {1 – 0,30} \direita)^t}$

Com $t$ em anos, substituindo $t$ na tabela a seguir dá

tempo em meses	tempo em anos	cálculos	Valor numérico
1	$\frac{1}{{12}}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}$	19414.289
12	1	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}$	14000
14	$\frac{7}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	13192.012
38	$\frac{{19}}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	6464.0859

Teachs.ru

Nuvem de tags

Avaliação

Visualizações

Comentários

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\left( {ab} \right)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) para cada \(a \ne 0\)

Valor de \(x\)
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Valor de \(x\)
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Tempo	Tempo dos anos (\(s\))	Capital acumulado, em milhares, invista com juros contínuos
Meio ano	\(s = \frac{1}{2}\)	\(10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
Dois anos	\(s = 2\)	\(10{\left( {1,00091667} \right)^{0,0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 meses	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

Ano	Tempo decorrido (\(t\))	Cálculo	População (milhões)
2021	0	\(P\left( t \right) = 126{\left( {1.0011} \right)^0}\)	126
2031	10	\(P\left( t \right) = 126{\left( {1.0011} \right)^{10}}\)	140.57
2051	30	\(P\left( t \right) = 126{\left( {1.0011} \right)^{30}}\)	174.95

Depósitos a prazo fixo	Taxa anual	períodos em um ano	taxa real	Dinheiro acumulado em \(k\) meses
dois meses	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}\)
três meses	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}\)
seis meses	1.56%	2	\(\frac{{1,56\% }}{4} = 0,78{\rm{\% }}\)	\(10000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}\)

Tempo	Número de períodos (\(k\))	Capital acumulado, em milhares, reinvestido a cada dois meses
Meio ano	3	\(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\)
Dois anos	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 meses	19	\(10{\left( {1.00091667} \right)^{19}} = 10.\;175612\)

tempo em meses	tempo em anos	cálculos	Valor numérico
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859