Definice exponenciální funkce

Exponenciální funkce modeluje různé přírodní jevy a sociální a ekonomické situace, proto je důležité exponenciální funkce identifikovat v různých kontextech.

Připomeňme, že pro číslo je definováno \({a^1} = a,{a^2} = aa,\;{a^3} = aaa\), obecně platí, že pro libovolné \(n\ ) přirozené číslo:

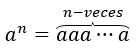
V případě \(a \ne 0\) máme toto: \({a^0} = 1,\;\) ve skutečnosti, když \(a \ne 0,\) má smysl provést operaci \ (\frac{a}{a} = 1;\) při aplikaci zákona o exponentech máme:

\(\frac{a}{a} = 1\)

\({a^{1 – 1}} = 1\)

\({a^0} = 1.\)

Když \(a = 0\), předchozí úvaha nedává smysl, proto výraz \({0^0},\) postrádá matematickou interpretaci.

V případě, že \(b > 0\) a platí, že \({b^n} = a,\), říká se, že \(b\) je n-tá odmocnina z \(a\) a je obvykle označované jako \ (b = {a^{\frac{1}{n}}},\;\) nebo \(b = \sqrt[n]{a}\).

Když \(a < 0\), neexistuje žádné reálné číslo \(b\) takové, že \({b^2} = a;\), protože \({b^2} \ge 0;\;\ ) tak výrazy formuláře \({a^{\frac{m}{n}}}\), nebude uvažováno pro \(a < 0.\) V následujícím algebraickém výrazu: \({a^n}\) \(a \ ) se nazývá základ a \(n\) je nazývá se exponent, \({a^n}\)se nazývá mocnina\(\;n\) z \(a\) nebo se také nazývá \(a\) k mocnině \(n,\;\)se dodržovat následující zákony z exponentů:

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\left( {ab} \right)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) pro každé \(a \ne 0\)

Exponenciální funkce má tvar:

\(f\left( x \right) = {a^x}\)

kde \(a > 0\) je konstanta a nezávislá proměnná je exponent \(x\).

Abychom mohli provést analýzu exponenciální funkce, budeme uvažovat tři případy

Případ 1 Když základ \(a = 1.\)

V tomto případě je \(a = 1,\) funkce \(f\left( x \right) = {a^x}\) konstantní funkcí.

Případ 2 Když základ \(a > 1\)

V tomto případě máme následující:

Hodnota \(x\)
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Funkce \(f\left( x \right) = {a^x}\) je přísně rostoucí funkce, to znamená, že pokud \({x_2} > {x_1}\), pak:

\({a^{{x_2}}} > a_{}^{{x_2}}\)

\(f\left( {{x_2}} \right) > f\left( {{x_1}} \right)\)

Když je jev modelován pomocí exponenciální funkce, s \(a > 1\), říkáme, že představuje exponenciální růst.

Případ 2 Když je základ \(a < 1\).

Hodnota \(x\)
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Když \(a < 1\), funkce \(f\left( x \right) = {a^x}\) je přísně klesající funkce, to znamená, když \({x_2} > {x_1}\ ), tak:

\({a^{{x_2}}} < a_{}^{{x_1}}\) \(f\left( {{x_2}} \right) < f\left( {{x_1}} \right) \) Když jev je modely s exponenciální funkcí, s \(a < 1\), říkáme, že představuje rozpad nebo pokles exponenciální. Následující graf ukazuje chování \({a^x}\) ve třech různých případech.

Aplikace exponenciální funkce

Příklad 1 Růst populace

Budeme označovat pomocí \({P_0}\) počáteční populaci a pomocí \(r \ge 0\) rychlost růstu populace, pokud míra populace zůstane v průběhu času konstantní; funkce

\(P\left( t \right) = {P_0}{\left( {1 + r} \right)^t};\)

Najděte populaci v čase t.

Praktický příklad 1

Populace Mexika v roce 2021 je 126 milionů a představuje roční nárůst o 1,1 %, Pokud se tento růst udrží, jaká populace bude v Mexiku v roce 2031, v roce 2021?

Řešení

V tomto případě \({P_o} = 126\) a \(r = \frac{{1.1}}{{100}} = 0.011\), takže byste měli použít:

\(P\left( t \right) = {P_0}{\left( {1 + .0011} \right)^t}\)

Následující tabulka ukazuje výsledky

Rok	uplynulý čas (\(t\))	Výpočet	Populace (miliony)
2021	0	\(P\left( t \right) = 126{\left( {1.0011} \right)^0}\)	126
2031	10	\(P\left( t \right) = 126{\left( {1.0011} \right)^{10}}\)	140.57
2051	30	\(P\left( t \right) = 126{\left( {1.0011} \right)^{30}}\)	174.95

Příklad 2 Výpočet složeného úroku

Banky nabízejí roční úrokovou sazbu, ale skutečná sazba závisí na tom, na kolik měsíců ji investujete; Pokud je vám například nabídnuta roční úroková sazba r %, skutečná měsíční sazba je \(\frac{r}{{12}}\) %, dvouměsíční sazba je \(\frac{r}{6}\)%, čtvrtletní je \(\frac{r}{4}\)%, čtvrtletní \(\frac{r}{3}\)% a semestr je \(\frac{r}{2}\)%.

Praktický příklad 2

Předpokládejme, že investujete 10 000 do banky a ona vám nabídne následující roční úrokové sazby:

Termínované vklady	Roční sazba	období v roce	skutečná sazba	Nashromážděné peníze za \(k\) měsíců
dva měsíce	0.55%	6	\(\frac{{0,55\% }}{6} = 0,091667{\rm{\% }}\)	\(10000{\left( {1 + 0,00091667} \right)^{\frac{k}{2}}}\)
tři měsíce	1.87%	4	\(\frac{{1,87\% }}{4} = 0,4675{\rm{\% }}\)	\(10000{\left( {1 + 0,00461667} \right)^{\frac{k}{3}}}\)
šest měsíců	1.56%	2	\(\frac{{1,56\% }}{4} = 0,78{\rm{\% }}\)	\(10 000{\left( {1 + 0,0078} \right)^{\frac{k}{6}}}\)

Číslo \(e\), Eulerův konstantní a nepřetržitý úrok.

Nyní předpokládejme, že máme počáteční kapitál \(C\) a investujeme jej s pevnou sazbou \(r > 0\) a rozdělíme rok na \(n\) období; kapitál nashromážděný za rok se rovná:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)

Abychom analyzovali, jak se akumulovaný kapitál chová, když \(n\), roste, přepíšeme akumulovaný kapitál za jeden rok:

\(A = \;C{\left( {1 + \frac{r}{n}} \right)^n}\)\(A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},\)

když uděláme \(m = \frac{n}{r}\), získáme:

\(A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}\)\(A = C{\left( {{{\left( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.\)

Jak roste \(n\), roste i \(m = \frac{n}{r}.\)

Jak \(m = \frac{n}{r},\) roste, výraz \({\left( {1 + \frac{1}{m}} \right)^m}\) se blíží tomu, co se nazývá Eulerova konstanta nebo číslo:

\(e \cca 2,718281828 \ldots .\)

Eulerova konstanta nemá konečný nebo periodický desetinný výraz.

Máme následující přiblížení

\(C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \approx C{e^r},\) \(C{\left( {1 + \frac{r}{n}} \right)^{ns}} \cca C{e^{rs}}.\)

K výrazu:

\(A = \;C{e^r},\)

Můžeme to interpretovat dvěma způsoby:

1.- Jako maximální částka, kterou můžeme nashromáždit za rok, když investujeme kapitál \(C,\;\) ročním tempem \(r.\)

2.- Jako částku, kterou bychom nashromáždili za rok, kdyby byl náš kapitál průběžně reinvestován ročním tempem \(r.\)

\(T\left( s \right) = \;C{e^{rs}},\)

je částka nashromážděná, pokud jsou \(s\) roky investovány s nepřetržitým úrokem.

Konkrétní příklad 3

Nyní se vrátíme k části konkrétního příkladu 2, kde je roční sazba 0,55 % ve dvouměsíčních splátkách. Vypočítejte kapitál, který se akumuluje, pokud je počáteční kapitál 10 000 a reinvestuje se půl roku, dva roky, 28 měsíců.

\(10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525\)

jak ukazuje tabulka níže, hodnota \(m = \frac{n}{r},\) není „malá“ a výše uvedená tabulka ukazuje, že \({\left( {1 + \frac{1}{ m}} \right)^m}\) je blízko Eulerově konstantě.

Čas	Počet období (\(k\))	Akumulovaný kapitál v tisících reinvestovaný každé dva měsíce
Půl roku	3	\(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\)
Dva roky	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 měsíců	19	\(10{\left( {1.00091667} \right)^{19}} = 10.\;175612\)

Čas	Čas v letech (\(s\))	Akumulovaný kapitál v tisících investujte s nepřetržitým úrokem
Půl roku	\(s = \frac{1}{2}\)	\(10{e^{0,0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
Dva roky	\(s = 2\)	\(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 měsíců	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

Příklad 2 Odpisy

Praktický příklad 1

Počítač odepisuje každý rok 30 %, pokud počítač stál 20 000 pesos, určete cenu počítače na \(t = 1,12,\;14,\;38\) měsíců.

V tomto případě má člověk:

\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^t}\)

Dosazením \(t\) v následující tabulce dostaneme \(t\) v letech

čas v měsících	čas v letech	výpočty	Číselná hodnota
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0,30} \right)^{\frac{7}{6}}}\)	6464.0859