Definition of Atmospheric Pressure

1. Force exerted by the weight of air -pressure- on the earth's surface, so that the higher the altitude relative to the ground, the lower the pressure. It is usually measured with a barometer, which is why the name barometric pressure is also seen.

Etymology: Pressure, by the Latin modes pressure, pressurenis.+ Atmosphere, from scientific Latin atmosphere, regarding the components of the Greek ἀτμός (atmosphere), which refers to 'air', and σφαῖρα (sphaira), as 'sphere', followed by the suffix -ico, in property of quality.
Cat. grammatical: noun fem.
in syllables: pressure + at-mos-fé-ri-ca.

Quote (APA)

Atmospheric pressure

Evelyn Maitee Marin | July 2022
Industrial Engineer, MSc in Physics, and EdD

Atmospheric pressure is the strength which applies the air of the atmosphere on the terrestrial surface, and therefore, on the bodies that are on it, starting from the basis of the concept of pressure, which is defined as the relationship between the magnitude of the force acting per unit of surface.

On the surface of the Earth, there is a gaseous layer that is made up of several gases and that vary in proportion and composition depending on the height and other factors. This mixture of gases forms what is known as "air", which has a density (since it has a mass and occupies a volume in space); As a consequence, the air column static that is above a body, will exert a force per unit area whose result is atmospheric pressure.

Background on atmospheric pressure

Although today the idea of ​​atmospheric pressure is something we take for granted, it has not always been an accepted and understood concept. It was not until 1643, when the physicist Evangelista Torricelli experimentally raised the idea of ​​the weight of air, although it should be noted that other Scientists such as Galileo Galilei and René Descartes had already laid the foundations that Torricelli materialized in his famous experiment with a tube of mercury.

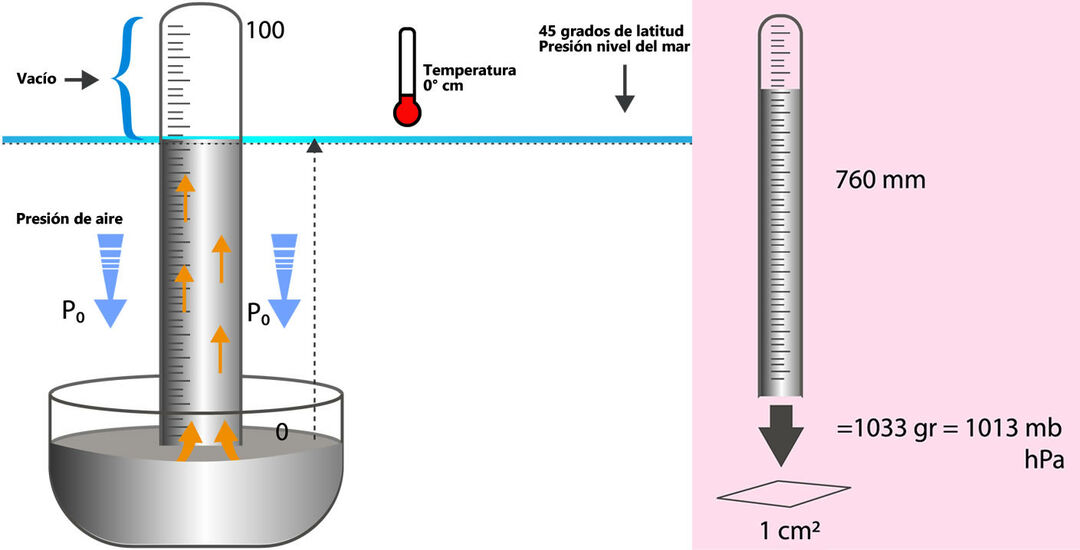
In Torricelli's experiment, the height of the mercury column in the tube was 760 mm

Galilei explained the limitation to raise a column of water by means of a propeller pump above 10.33 m in height, alluding that it was due to the terror of emptiness (horror vacuis) exerted by a force equivalent to a column of 10.33 m of water, calling this height the limit (altezza limitissima).

For his part, René Descartes published a letter in 1638 where he referred to the weight of the air, and compared it to a wool blanket that covers the Earth even above the clouds, whose weight can compress the surface of a bucket of mercury, preventing the column of this element from descending.

From all these findings and thanks to Torricelli's experiment, the Torricelli tube was developed, and served as a reference for the studies of Blaise Pascal and the German Otto von Guericke, who in 1654 publicly demonstrated the existence of atmospheric pressure.

Instruments and pressure units

Atmospheric pressure can be measured using a barometer. There are several types of barometers, among the best known are the mercury barometer and the aneroid barometer (without mercury).

As for pressure units, the most common are:

• In the international system of units: Pascal (Pa)
• In English system: Psi (lbf/in2)

Other units:

or mm of Mercury (mmHg)
or Atmosphere (atm)

At sea level, normal atmospheric pressure is 101,325 Pa (N/m2), or its equivalent of 760 mm Hg or 1 atm.

Some conversion factors for pressure units are:

1 Pa = 105 bar

1Psi = 6895Pa

Variation of atmospheric pressure with height

Since atmospheric pressure is due to the weight per unit area exerted by the column of air above the object of study, up to the limits of the earth's atmosphere, it is logical to deduce that the greater the height at which the object is with respect to the surface of the Earth, the smaller the column of air that will exert pressure on it, for this reason, the atmospheric pressure depends on the height, which in turn affects the temperature which affects the density of the air.

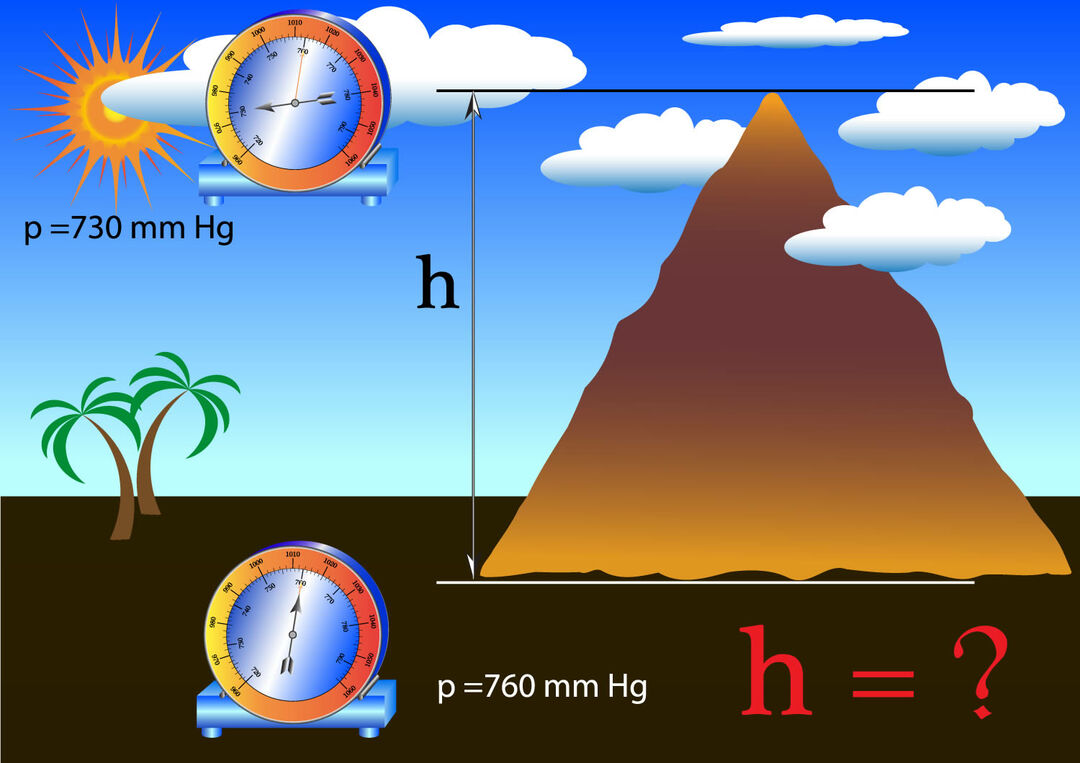
on top of a mountain atmospheric pressure is lower than at sea level

If the density of the air and the height of the object of study with respect to the atmosphere are known, the local atmospheric pressure can be determined by means of the expression:

\({{P}_{atm}}=Height~of~atm\acute{o}sphere\times density~of~air\times gravity\)

For example, if you want to determine the atmospheric pressure of a region that is 9000 m above sea level, atmosphere, where the air density is 1.3 kg/m3 and the local gravity is 9.81 m/s2, the result will be:

\({{P}_{atm}}=9000~m\times 1.3~{}^{kg}\!\!\diagup\!\!{}_{{{m}^{3}} }\;\times 9.81~{}^{m}\!\!\diagup\!\!{}_{{{s}^{2}}}\;\)

\({{P}_{atm}}=114777{}^{N}\!\!\diagup\!\!{}_{{{m}^{2}}}\;\)

That is, the atmospheric pressure would be 114777 Pa